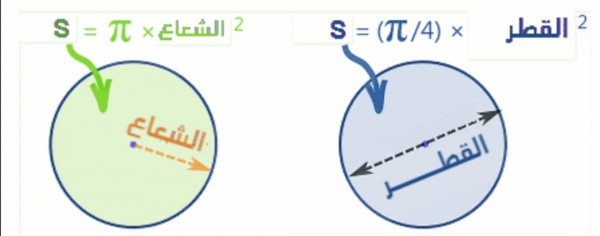
ما هو شعاع قرص مساحته ٣١٥ سنتيمتر مربع
مساحة القرص تساوي π r2
حيث أن r ترمز إلى شعاع القرص
π هي قيمة ثابتة تساوي ٢٢/ ٧ أو ٣.١٤١٥٩
بمعنى أن مساحة القرص تساوي شعاع القرص تربيع مضروباََ في ٣.١٤١٥٩
ويتم تعريف مساحة القرص على أنها المساحة الداخلية الموجودة في أي دائرة.
ولمعرفة كم يساوي شعاع القرص يتم استخدام قانون مساحة القرص لاستنتاج شعاع القرص منه.
وبذلك تكون طريقة الحل كالتالي :
مساحة القرص = π r2
315 = r2 * 3.14159
r2 = 315 / 3.14159
r2 = 100.26769884039
بأخذ الجذر التربيعي للطرفين
r = +- 10.01337106
وبم أن هذا الرقم يجب أن يكون موجب لأنه لا يوجد قياس بالسالب
اذاََ
r= 10.01337106
أي ما يساوي 10 سنتيمتر تقريباََ
إذا شعاع القرص يساوي 10 سنتيمتر تقريباََ.
الدائرة أو القرص هي شكل من الأشكال الهندسية تتميز بكونها شكل منتظم، وهي عبارة عن نقاط متصلة ببعضها، ولها بعد ثابت عن نقطة تسمى بمركز الدائرة.
يوجد الدائرة أو القرص مصطلحات ثابتة وهي :
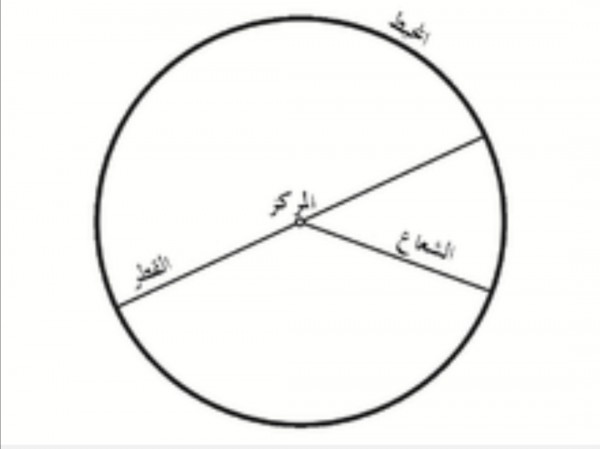
نق - أو ما يطلق عليها نصف القطر ،وهي عبارة عن البُعد بين مركز الدائرة وإلاطار الخارجي الدائرة ،ودائما يكون رقم ثابت الدائرة الواحدة، فإذا قمت بقياس نصف قطر الدائرة من مركزها إلى أي نقطة فيكون رقم ثابت، كما يطلق أيضاََ على نصف القطر ( شعاع)
ق - وهو اختصار لكلمة قطر الدائرة ؛ وهو عبارة عن طول أي نقطتين على الدائرة مروراََ بمركز الدائرة.
ط - وهو قيمة تقريبية تساوي 22/7
محيط الدائرة يساوي 2 * نق * ط
أو
ق * ط
مساحة الدائرة تساوي
نق٢ * ط
و بذلك لحساب المحيط أو المساحة يستلزم معرفة قطر الدائرة أو نصف قطرها
واذا كان من المعطيات القطر ونريد نصف القطر نقوم بقسمته على ٢